Basics of Visible and Infrared Remote Sensing

Radiative Transfer Equationn »Introduction

Radiation detected by the satellite may have both surface and atmospheric contributions. Notice that radiation comes from different heights in the atmosphere.

Note that in this chapter, radiance is represented by R(λ) instead of I(λ).

Radiative Transfer Equation »Beer's Law 1

Radiation from the earth’s surface and from layers in the atmosphere is transmitted through the atmosphere to reach the satellite.

Beer's Law describes how energy is transmitted to the satellite from the surface or from a layer in the atmosphere.

The second equation shows the relationship between transmittance, represented by τ, and optical depth, represented by k(λ)u.

Optical depth is a measure of the opaqueness of a given atmospheric layer. The negative exponent means that as the optical depth increases, the transmittance decreases exponentially.

u is proportional to the number of absorbing molecules between the emitting source and the top of the atmosphere and is referred to as the density weighted path length. k is a measure of the efficiency of molecular attenuation at wavelength λ.

Radiative Transfer Equation »Beer's Law 2

Consider an atmospheric layer and a wavelength where absorption occurs, that is, where k(λ) does not equal zero. The density of the atmosphere above layer p determines u, the density weighted path length. The graph on the left shows transmittance as a function of u. As u decreases, tau, the transmittance, increases, and therefore more of the energy emitted from layer p will reach the top of the atmosphere.

Radiative Transfer Equation »Weighting Function Contribution - Low Atmosphere

The weighting function for radiation at a given wavelength is shown on the right. It represents contributions from various atmospheric layers to the radiance reaching the top of the atmosphere.

The highlighted yellow area of the graphic on the left shows the contribution from the lowest levels of the atmosphere to the radiance reaching the top of the atmosphere.

As shown in the graphic, there is a substantial amount of energy available in the lower atmosphere, but only a small amount reaches the top of the atmosphere as indicated by the narrow band. This is due to the large optical depth that this radiation passes through.

Radiative Transfer Equation »Weighting Function Contributions - Mid Atmosphere

The graph on the left shows the transmitted energy emitted from higher in the atmosphere. Although there is less energy available here because the atmosphere cools with height, there is also an increase in transmittance because there are less absorbing constituents in the atmosphere above this layer. This results in a much greater percentage of energy from this level reaching the top of the atmosphere. The greater radiance contribution is shown by the wider bar at the top of the left figure. Radiance from this pressure level is associated with the weighting function's peak value.

Radiative Transfer Equation »Weighting Function Contributions - High Atmosphere

The graph on the left shows the radiance contributed by an upper tropospheric layer. Here transmittance to the top of the atmosphere is large, but the layer's radiance is small. Hence, there is a small contribution to the weighting function on the right.

Radiative Transfer Equation »Water Vapour Channel: Weighting Function and Image

The 6.7 µm channel weighting function is given on the left.

A 6.7 µm channel image is given on the right. This channel is very sensitive to water vapour and receives the majority of its radiance from the mid and upper atmosphere.

Dark regions are radiance from lower in the atmosphere (dry, warm) and light regions are from higher in the atmosphere (moist, cold) or from cloud tops.

Radiative Transfer Equation »Long Wave Infrared Channel: Weighting Function and Image

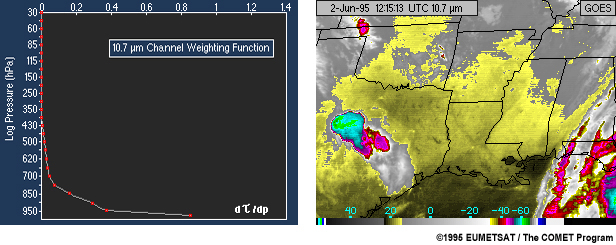
The GOES longwave infrared window (10.7 µm) channel weighting function is given on the left.

A 10.7 µm channel image is given on the right. This is a window channel and receives the majority of its radiance from the earth's surface and clouds when they are present.

Radiative Transfer Equation »"Dirty" Window Channel: Weighting Function and Image

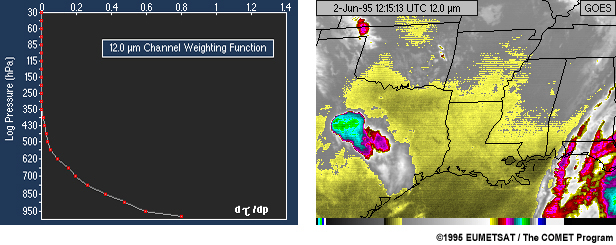
The GOES "dirty" window (12 µm) channel weighting function is given on the left. Compare it to the 10.7 µm channel weighting function on the previous page.

A 12 µm channel image is given on the right. This window channel is sensitive to low level moisture when it is present. In a dry atmosphere, this channel looks very similar to the 10.7 µm channel.

It is instructive to toggle between current and previous pages and observe the difference in surface temperature between the two channels. This difference is due to low level moisture.

Note that this channel is available on the Meteosat Second Generation satellite series.

Radiative Transfer Equation »Surface Contribution Term

The infrared radiance detected by a satellite is emitted from both the surface of the earth and the atmosphere. The radiance from the surface is given as the product of its black body radiance, the emissivity of the surface at the given wavelength, and the transmittance from the surface to the top of the atmosphere. Most surfaces have a thermal emissivity near one.

Radiative Transfer Equation »Atmospheric Contribution Term

The radiance from an atmospheric layer is given as the product of its blackbody radiance, emissivity, and the transmittance from that layer to the top of the atmosphere. The sum of these layers is the atmospheric contribution at a given wavelength.

Radiative Transfer Equation »Complete Equation

The total emitted upwelling radiance is the sum of the atmospheric and surface contributions. The atmospheric contribution can also be written as an integral over pressure where the emissivity and transmittance terms become the weighting function, dτ /dp.

Radiative Transfer Equation »Summary

Summary:

• Earth emitted radiance must pass through the atmosphere, which selectively absorbs and emits infrared radiation
• Beer's Law describes the radiance attenuation as a function of the absorbing strength and number of molecules between the source (earth and atmosphere) and the sensor (satellite)
• Weighting functions indicate the contribution to the outgoing radiance from various layers of the atmosphere
• Weighting functions for infrared windows peak at the earth's surface, as they primarily receive radiation from the earth's surface in cloud-free conditions
• The radiative transfer equation summarizes the radiance from both the surface and different layers in the atmosphere

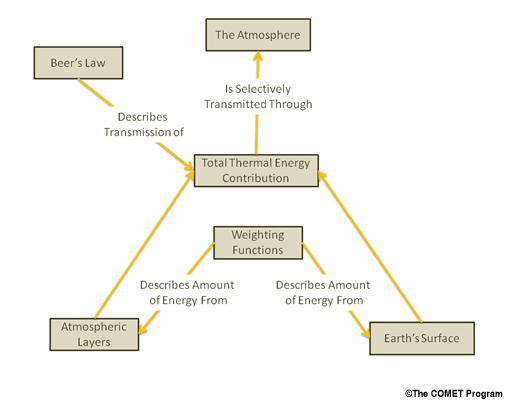
Concept Map »Concept Map

Review the concept map for this section. You can get more information about each topic by clicking on its box. (You will be sent to another page in this section; click the Back button to return here.)