The time taken by a satellite to travel around its orbit once is known as the period, T. From Newton's laws it is relatively simple to show that the period of an orbit simply depends on its altitude. In other words, for any given height above the Earth's surface (strictly speaking, distance from the Earth's centre) a satellite will take a fixed time to complete an orbit, regardless of the mass of the satellite.
Associated with this is the idea of orbital speed. This too is dependent only on the altitude of the satellite. So, whether the spacecraft is as massive as the Mir space-station or as small as Sputnik, its orbital speed and period will be the same for any given height above the surface. If the spacecraft changes its speed, its altitude will also change. The animation below shows two satellites at different altitudes. Click on the black area to start the motion.
As the animation shows, spacecraft at higher altitudes travel slower than those at lower altitudes. The equation which enables us to calculate a satellite's orbital period is:
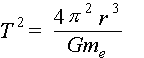 |
where
|
If we are interested in heights above the surface, then we can simply say r = rE + h , where rE = 6378 km
Try doing a quick calculation yourself of the period of an orbit of altitude 850 km (this is the approximate average height of the current NOAA satellites).
Use the applet below to calculate the periods for any height (in km). See if you can use this to work out the height that's necessary for an orbital period of 24 hours. Type a height (in km) into the upper box. The time period corresponding to this height will then be displayed in the lower box.